Différence entre les transformations de Laplace et de Fourier
 Share
Share
Laplace vs Fourier Transforms
Les transformées de Laplace et de Fourier sont des transformées intégrales, qui sont le plus souvent utilisées comme méthodes mathématiques pour résoudre des systèmes physiques modélisés mathématiquement. Le processus est simple Un modèle mathématique complexe est converti en un modèle plus simple, pouvant être résolu à l'aide d'une transformation intégrale. Une fois le modèle plus simple résolu, la transformation intégrale inverse est appliquée, ce qui fournirait la solution au modèle original..
Par exemple, étant donné que la plupart des systèmes physiques donnent lieu à des équations différentielles, ils peuvent être convertis en équations algébriques ou en équations différentielles de degré inférieur faciles à résoudre à l’aide d’une transformation intégrale. Alors résoudre le problème deviendra plus facile.
Quelle est la transformation de Laplace?
Étant donné une fonction F (t) d'une variable réelle t, sa transformation de Laplace est définie par l'intégrale 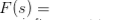 (chaque fois qu'il existe), fonction d'une variable complexe s. Il est généralement noté L F (t). La transformation inverse de Laplace d'une fonction F(s) est considéré comme la fonction F (t) de telle sorte que L F (t) = F(s), et dans la notation mathématique habituelle nous écrivons, L -1F(s) = F (t).La transformation inverse peut être rendue unique si les fonctions null ne sont pas autorisées. On peut identifier ces deux opérateurs comme des opérateurs linéaires définis dans l'espace des fonctions, et il est également facile de voir que L -1L F (t) = F (t), si les fonctions null ne sont pas autorisées.
(chaque fois qu'il existe), fonction d'une variable complexe s. Il est généralement noté L F (t). La transformation inverse de Laplace d'une fonction F(s) est considéré comme la fonction F (t) de telle sorte que L F (t) = F(s), et dans la notation mathématique habituelle nous écrivons, L -1F(s) = F (t).La transformation inverse peut être rendue unique si les fonctions null ne sont pas autorisées. On peut identifier ces deux opérateurs comme des opérateurs linéaires définis dans l'espace des fonctions, et il est également facile de voir que L -1L F (t) = F (t), si les fonctions null ne sont pas autorisées.
Le tableau suivant répertorie les transformations de Laplace de certaines des fonctions les plus courantes..

Qu'est-ce que la transformée de Fourier?
Étant donné une fonction F (t) d'une variable réelle t, sa transformation de Laplace est définie par l'intégrale 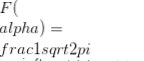 (à chaque fois qu'il existe), et est généralement désigné par F F (t). La transformée inverse F -1F(α) est donné par l'intégrale
(à chaque fois qu'il existe), et est généralement désigné par F F (t). La transformée inverse F -1F(α) est donné par l'intégrale  . La transformée de Fourier est également linéaire et peut être considérée comme un opérateur défini dans l'espace des fonctions..
. La transformée de Fourier est également linéaire et peut être considérée comme un opérateur défini dans l'espace des fonctions..
En utilisant la transformée de Fourier, la fonction d'origine peut être écrite comme suit à condition que la fonction ne comporte qu'un nombre fini de discontinuités et qu'elle soit parfaitement intégrable.. 
Quelle est la différence entre les transformations de Laplace et de Fourier?
- Transformée de Fourier d'une fonction F (t) est défini comme
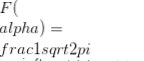 , alors que la laplace transform est définie pour être
, alors que la laplace transform est définie pour être 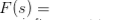 .
. - La transformée de Fourier est définie uniquement pour les fonctions définies pour tous les nombres réels, tandis que la transformation de Laplace ne nécessite pas que la fonction soit définie pour définir les nombres réels négatifs..
- La transformée de Fourier est un cas particulier de la transformée de Laplace. On peut voir que les deux coïncident pour des nombres réels non négatifs. (c'est-à-dire prendre s à laplace pour être iα + β où α et β sont réels tels que e β= 1/√ (2ᴫ))
- Chaque fonction ayant une transformation de Fourier aura une transformation de Laplace mais pas l'inverse..
