Différence entre égal et équivalent
 Share
Share
Différence principale - Égal ou équivalent
Égal et équivalent sont des termes fréquemment utilisés en mathématiques. le différence principale entre égal et équivalent est que le terme égale se réfère à des choses qui sont similaires dans tous les aspects, alors que le terme équivalent fait référence à des choses similaires dans un aspect particulier. Notez que dans le théorie des ensembles, les mots «égal» et «équivalent» ont des significations spécifiques, comme nous le verrons plus loin.
Que signifie égal
En général, deux choses sont égales si elles sont similaires à tous égards.
Dans le cas de la théorie des ensembles, deux ensembles sont égaux s'ils contiennent tous deux les mêmes éléments. le ordre dans lequel ils sont répertoriés dans un ensemble n'a pas d'importance. Par exemple, supposons
 et
et
 puis,
puis,
l'ensemble  est égal à l'ensemble
est égal à l'ensemble  .
.
Que signifie équivalent
On peut dire que deux choses sont équivalentes si elles sont similaires dans des conditions particulières. Par conséquent, si deux entités sont équivalent en grande partie dépend à la condition que nous utilisons pour décrire leur équivalence. Par exemple, les nombres 2 et 7 sont équivalents en ce sens qu'ils sont tous deux des nombres premiers. Cependant, si la condition qui nous intéresse est de savoir si les nombres sont pairs, alors en ce sens, 2 et 7 sont ne pas équivalent. Nous utilisons les symboles  ou
ou  pour indiquer que
pour indiquer que  et
et  sont équivalents.
sont équivalents.
Une fois qu'un critère a été défini, les éléments équivalents satisfont aux relations d'équivalence:
- Réflexivité:
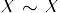
- Symétrie: Si
 , puis
, puis 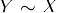
- Transitivité: Si
 et
et 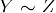 , puis
, puis 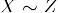
En théorie des ensembles, deux ensembles sont équivalent s'ils ont le même nombre d'éléments. Les éléments eux-mêmes n'ont pas besoin d'être identiques, que ce soit, seulement le nombre d'éléments doit être identique. Par exemple, supposons
 et
et
 puis,
puis,
les ensembles  et
et  sont équivalents.
sont équivalents.

Symboles pour exprimer l'égalité et l'équivalence
Différence entre égal et équivalent
Sens général
Quand deux choses sont égal, ils sont similaires dans tous les aspects.
Quand les choses sont équivalent, ils sont similaires dans un aspect particulier.
En théorie des ensembles
Quand deux ensembles sont égal, ils contiennent les mêmes éléments.
Quand deux ensembles sont équivalent, ils contiennent le même nombre de éléments.
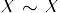
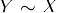
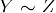 , puis
, puis