Comment calculer la demi-vie
 Share
Share
Dans cette section, nous étudierons la demi-vie et en déduirons la formule permettant de calculer la demi-vie. En radioactivité, demi vie est le temps pris par la moitié des noyaux radioactifs dans un échantillon d'isotope radioactif. Le nombre de noyaux radioactifs dans un échantillon décroît de manière exponentielle dans le temps. Pour calculer la demi-vie, on utilise donc les mathématiques de la décroissance exponentielle. La demi-vie est un concept extrêmement important pour les applications de la radioactivité. Les radio-isotopes introduits dans les organes en radiothérapie, par exemple, ne doivent pas rester trop longtemps dans le corps du patient. D'autre part, les isotopes utilisés pour dater les artefacts historiques doivent avoir une longue vie, de sorte qu'il en reste assez jusqu'à ce jour pour que nous puissions déterminer l'âge des objets..
Différence entre la nature aléatoire et spontanée de la désintégration radioactive
La désintégration radioactive est classée dans les deux catégories au hasard et spontané.
- La décroissance radioactive est aléatoire parce que nous ne pouvons pas déterminer quand un noyau donné va se désintégrer, ou déterminer combien de temps cela prendrait avant qu'un noyau donné ne se désintègre. Par conséquent, chaque noyau radioactif dans un échantillon a la même probabilité de décroissance à un moment donné.
- La désintégration radioactive est spontanée parce qu'il n'est pas affecté par les conditions extérieures.
Quelle est la moitié de la vie
Le nombre de noyaux radioactifs dans un échantillon diminue, car une fois que le noyau se désintègre en décomposition alpha, bêta et gamma, il ne peut plus subir le même processus de désintégration. Le nombre de noyaux radioactifs dans l'échantillon diminue de manière exponentielle.
le activité, ou la taux de décomposition,est le taux de changement du nombre de noyaux radioactifs. Ceci est donné par,

Le signe négatif signifie que le nombre de noyaux radioactifs dans un échantillon est décroissant heures supplémentaires. $ latex \ lambda & s = 1 $ est appelé le constante de décomposition. Il donne la probabilité qu'un noyau donné se désintègre par unité de temps. La constante de désintégration a une valeur spécifique pour tout processus de désintégration nucléaire donné. Plus le  , plus la probabilité de désintégration est élevée et plus le nombre de noyaux radioactifs dans l'échantillon diminue rapidement..
, plus la probabilité de désintégration est élevée et plus le nombre de noyaux radioactifs dans l'échantillon diminue rapidement..
Si le nombre de noyaux radioactifs dans un échantillon à la fois  est
est  , alors le nombre de noyaux radioactifs
, alors le nombre de noyaux radioactifs  dans l'échantillon après un temps
dans l'échantillon après un temps  est donné par:
est donné par:

Le nombre de noyaux radioactifs dans l'échantillon diminue de manière exponentielle. Demi vie ( ) Est la durée nécessaire pour que le nombre de noyaux radioactifs se réduise de moitié. Si nous traçons un graphique de la façon dont le nombre de noyaux radioactifs dans l'échantillon varie dans le temps, nous obtenons le graphique suivant:
) Est la durée nécessaire pour que le nombre de noyaux radioactifs se réduise de moitié. Si nous traçons un graphique de la façon dont le nombre de noyaux radioactifs dans l'échantillon varie dans le temps, nous obtenons le graphique suivant:

Comment calculer la demi-vie - courbe de décroissance radioactive
Comment calculer l'activité
L'activité de l'échantillon est proportionnelle au nombre de noyaux radioactifs présents. Donc, nous pouvons faire une déclaration équivalente,

où  est l'activité de l'échantillon au moment
est l'activité de l'échantillon au moment  , avec
, avec  l'activité quand
l'activité quand  .
.
Si un graphique d'activité en fonction du temps est dessiné, il produira un graphique ayant la même forme (c'est-à-dire que l'activité diminue également de manière exponentielle)..
L'activité est mesurée avec l'unité SI becquerel (Bq). Une activité de 1 Bq correspond à un taux de 1 décroissance par seconde. le curie (Ci) est une autre unité utilisée pour mesurer l'activité. 1 Ci = 3,7 × 10dix Bq.
Formule demi vie
Nous allons maintenant dériver une formule pour obtenir la demi-vie de la constante de désintégration. On commence avec,

Après un certain temps  , le nombre de moitiés de noyaux radioactifs. Alors,
, le nombre de moitiés de noyaux radioactifs. Alors,  , ou
, ou

En prenant le logarithme naturel des deux côtés, on obtient:

et donc,

Comment calculer la demi-vie
Exemple 1
L'indium-112 a une demi-vie de 14,4 minutes. Un échantillon contient 1,32 × 1024 les atomes d'indium-112.
a) Trouver la constante de désintégration
b) Déterminez combien d’atomes d’Indium-112 resteraient dans l’échantillon après 1 heure.
a) depuis  ,
,

b) Utilisation  ,
,  des atomes.
des atomes.
Exemple 2
Au cours d’un traitement contre le cancer de la thyroïde, un patient reçoit un échantillon d’iode-131 à ingérer, d’une activité de 1,10 MBq. La demi-vie de l'iode 131 est de 8,02 jours. Retrouvez l'activité de l'iode 131 dans le corps du patient après 5 jours d'ingestion.
Nous utilisons  . Tout d'abord, nous travaillons
. Tout d'abord, nous travaillons  :
:

ensuite,
 Mbq.
Mbq.
Remarque:
- Nous avons directement calculé la constante de désintégration par jour et conservé la demi-vie également en jours. Donc, les jours annulés lorsque nous avons calculé
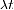 et il n'y avait pas besoin de convertir les temps en secondes (cela aurait fonctionné aussi bien, mais cela aurait impliqué un peu plus de calcul)
et il n'y avait pas besoin de convertir les temps en secondes (cela aurait fonctionné aussi bien, mais cela aurait impliqué un peu plus de calcul) - En réalité, l'activité serait plus petite. Cela est dû au fait qu’il existe également une demi-vie biologique. C'est la vitesse à laquelle le patient excrète des noyaux radioactifs de son corps.
Exemple 3
Calculer la demi-vie d'un isotope radioactif dont l'activité est réduite de 4% sur 1000 ans.
4% = 0,04. Nous avons maintenant
 . Prenant ln des deux côtés,
. Prenant ln des deux côtés,
 par an.
par an.
 216 ans.
216 ans.
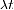 et il n'y avait pas besoin de convertir les temps en secondes (cela aurait fonctionné aussi bien, mais cela aurait impliqué un peu plus de calcul)
et il n'y avait pas besoin de convertir les temps en secondes (cela aurait fonctionné aussi bien, mais cela aurait impliqué un peu plus de calcul)