Différence entre moyenne et médiane
 Share
Share
 La tendance centrale implique la tendance des points de données à se regrouper autour de sa valeur centrale ou centrale. Les deux mesures de la tendance centrale les plus couramment utilisées sont la moyenne et la médiane.. Signifier est définie comme la valeur "centrale" de l'ensemble de données donné, alors que médian est la valeur "la plus moyenne" dans l'ensemble de données donné.
La tendance centrale implique la tendance des points de données à se regrouper autour de sa valeur centrale ou centrale. Les deux mesures de la tendance centrale les plus couramment utilisées sont la moyenne et la médiane.. Signifier est définie comme la valeur "centrale" de l'ensemble de données donné, alors que médian est la valeur "la plus moyenne" dans l'ensemble de données donné.
Une mesure idéale de la tendance centrale est une mesure clairement définie, facile à comprendre, simplement calculable. Elle devrait être basée sur toutes les observations et moins affectée par les observations extrêmes présentes dans l’ensemble de données..
Les gens opposent souvent ces deux mesures, mais le fait est qu'elles sont différentes. Cet article souligne spécifiquement les différences fondamentales entre moyenne et médiane. Regarde.
Contenu: Moyenne vs médiane
Tableau de comparaison
| Base de comparaison | Signifier | Médian |
|---|---|---|
| Sens | La moyenne correspond à la moyenne simple de l'ensemble de valeurs ou de quantités donné. | La médiane est définie comme le nombre du milieu dans une liste de valeurs ordonnée. |
| Qu'Est-ce que c'est? | C'est une moyenne arithmétique. | C'est la position moyenne. |
| Représente | Centre de gravité de l'ensemble de données | Centre de gravité de l'ensemble de données Point médian du jeu de données |
| Applicabilité | Distribution normale | Distribution asymétrique |
| Les valeurs aberrantes | La moyenne est sensible aux valeurs aberrantes. | La médiane n'est pas sensible aux valeurs aberrantes. |
| Calcul | La moyenne est calculée en additionnant toutes les observations et en divisant la valeur obtenue par le nombre d'observations.. | Pour calculer la médiane, le jeu de données est classé par ordre croissant ou décroissant, puis la valeur située au milieu du nouvel ensemble de données est la médiane.. |
Définition de moyenne
La moyenne est la mesure largement utilisée de la tendance centrale, définie comme la moyenne de l'ensemble des valeurs. Il représente le modèle et la valeur la plus courante de la plage de valeurs donnée. Il peut être calculé à la fois en séries discrètes et continues..
La moyenne est égale à la somme de toutes les observations divisée par le nombre d'observations dans l'ensemble de données. Si la valeur assumée par une variable est égale, sa moyenne sera également la même. La moyenne peut être de deux types, la moyenne de l'échantillon (x̅) et la moyenne de la population (µ). Il peut être calculé avec la formule donnée:
- Moyenne arithmétique:
 où Ʃ = lettre grecque sigma, désigne la «somme de…»
où Ʃ = lettre grecque sigma, désigne la «somme de…»
n = nombre de valeurs - Pour les séries discrètes:
 où, f = fréquence
où, f = fréquence - Pour les services continus:
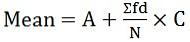 où d = (X-A) / C
où d = (X-A) / C
A = moyenne supposée
C = diviseur commun
Définition de la médiane
La médiane est une autre mesure importante de la tendance centrale utilisée pour diviser la valeur en deux parties égales, à savoir la moitié supérieure de l’échantillon, la population ou la distribution de probabilité de la moitié inférieure. Il s'agit de la valeur la plus moyenne, obtenue lorsque les observations sont triées dans un ordre spécifique, croissant ou décroissant..
Pour le calcul de la médiane, tout d’abord, organisez les observations en ordre décroissant, puis appliquez la formule appropriée, conformément aux conditions indiquées ci-dessous:
- Si le nombre d'observations est impair:
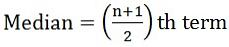 où n = nombre d'observations
où n = nombre d'observations - Si le nombre d'observations est même:
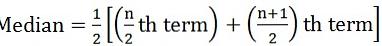
- Pour les séries continues:
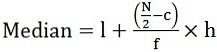 où l = limite inférieure de la classe médiane
où l = limite inférieure de la classe médiane
c = fréquence cumulée de la classe médiane précédente
f = fréquence de la classe médiane
h = largeur de classe
Principales différences entre la moyenne et la médiane
Les différences significatives entre la moyenne et la médiane sont fournies dans l'article ci-dessous:
- En statistique, une moyenne est définie comme la moyenne simple d'un ensemble donné de valeurs ou de quantités. La médiane est le nombre du milieu dans une liste de valeurs ordonnée.
- Alors que la moyenne est la moyenne arithmétique, la médiane est la moyenne positionnelle. En substance, la position de l'ensemble de données détermine la valeur de la médiane..
- La moyenne indique le centre de gravité de l'ensemble de données, tandis que la médiane met en évidence la valeur la plus moyenne de l'ensemble de données..
- La moyenne convient aux données distribuées normalement. À l'opposé, la médiane est meilleure lorsque la distribution des données est asymétrique..
- La moyenne est fortement affectée par la valeur extrême qui n’est pas dans le cas d’une médiane.
- La moyenne est calculée en additionnant toutes les observations puis en divisant la valeur obtenue par le nombre d'observations; le résultat est moyen. Par opposition à la médiane, le jeu de données est organisé dans un ordre croissant ou décroissant. La valeur située exactement au milieu du nouvel ensemble de données est la médiane..
Exemple
Trouvez la moyenne et la médiane de l'ensemble de données donné:
58, 26, 65, 34, 78, 44, 96
Solution: Pour calculer la moyenne, vous devez diviser la somme des observations par le nombre d'observations.,

 Moyenne = 57,28
Moyenne = 57,28
Pour calculer la médiane, tout d’abord, organisez la série dans une séquence, c’est-à-dire du plus bas au plus élevé,
26, 34, 44, 58, 65, 78, 96
 où n = nombre d'observations
où n = nombre d'observations
Conclusion
Après avoir passé en revue les points ci-dessus, nous pouvons dire que ces deux concepts mathématiques sont différents. La moyenne arithmétique ou moyenne est considérée comme la meilleure mesure de la tendance centrale car elle contient toutes les caractéristiques d'une mesure idéale, mais elle présente l'inconvénient que les fluctuations de l'échantillonnage influent sur la moyenne..
De la même manière, la médiane est également définie sans difficulté et facile à comprendre et à calculer, et le meilleur atout de cette mesure est qu’elle n’est pas affectée par les fluctuations de l’échantillonnage, mais le seul inconvénient de la médiane est qu’elle ne repose pas sur observations. Pour la classification open end, la médiane est généralement préférable à la moyenne.
 où Ʃ = lettre grecque sigma, désigne la «somme de…»
où Ʃ = lettre grecque sigma, désigne la «somme de…» où, f = fréquence
où, f = fréquence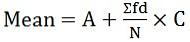 où d = (X-A) / C
où d = (X-A) / C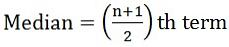 où n = nombre d'observations
où n = nombre d'observations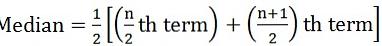
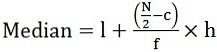 où l = limite inférieure de la classe médiane
où l = limite inférieure de la classe médiane Médiane = 4th terme = 58
Médiane = 4th terme = 58