Différence entre T-test et ANOVA
 Share
Share
 La ligne de démarcation est mince entre le test t et l’ANOVA, c’est-à-dire lorsque la moyenne de la population de deux groupes seulement doit être comparée, le test t est utilisé, mais lorsque les moyennes de plus de deux groupes doivent être comparées, ANOVA est préféré.
La ligne de démarcation est mince entre le test t et l’ANOVA, c’est-à-dire lorsque la moyenne de la population de deux groupes seulement doit être comparée, le test t est utilisé, mais lorsque les moyennes de plus de deux groupes doivent être comparées, ANOVA est préféré.
Le test T et l'analyse de la variance, abrégés en ANOVA, sont deux techniques statistiques paramétriques utilisées pour vérifier l'hypothèse. Celles-ci reposent sur l'hypothèse courante voulant que la population de l'échantillon soit normalement distribuée, homogénéité de la variance, échantillonnage aléatoire des données, indépendance des observations, mesure de la variable dépendante au niveau du ratio ou de l'intervalle, ce que les gens interprètent souvent mal deux.
Voici un article qui vous est présenté pour vous permettre de comprendre la différence significative entre le test t et l’ANOVA..
Contenu: ANOVA T-test vs
Tableau de comparaison
| Base de comparaison | Test t | ANOVA |
|---|---|---|
| Sens | Le test T est un test d'hypothèse utilisé pour comparer les moyennes de deux populations. | L'ANOVA est une technique statistique utilisée pour comparer les moyennes de plus de deux populations.. |
| Statistique de test | (x µ-µ) / (s / √n) | Entre variance d'échantillon / Variance intra-échantillon |
Définition du test t
Le test t est décrit comme le test statistique qui examine si les moyennes de population de deux échantillons diffèrent considérablement l'un de l'autre, en utilisant la distribution t qui est utilisée lorsque l'écart type n'est pas connu et que la taille de l'échantillon est petite. C'est un outil pour analyser si les deux échantillons sont tirés de la même population.
Le test est basé sur la statistique t, qui suppose que la variable est normalement distribuée (distribution en forme de cloche symétrique) et que la moyenne est connue et que la variance de la population est calculée à partir de l'échantillon..
Dans le test t, l'hypothèse nulle prend la forme de H0: µ (x) = µ (y) contre l'hypothèse alternative H1: µ (x) ≠ µ (y), où µ (x) et µ (y) représentent les moyennes de la population. Le degré de liberté du test t est n1 + n2 - 2
Définition de ANOVA
L'analyse de variance (ANOVA) est une méthode statistique couramment utilisée dans toutes les situations dans lesquelles une comparaison doit être faite entre plus de deux moyennes de population, comme le rendement de la culture à partir de plusieurs variétés de semences. C’est un outil d’analyse essentiel pour le chercheur qui lui permet de réaliser simultanément des tests. Lorsque nous utilisons l'ANOVA, on suppose que l'échantillon est tiré de la population normalement distribuée et que la variance de la population est égale..
Dans ANOVA, la quantité totale de variation dans un jeu de données est divisée en deux types, à savoir la quantité affectée au hasard et la quantité affectée à des causes particulières. Son principe de base est de tester les variances entre les moyennes de la population en évaluant la quantité de variation dans les éléments de groupe, proportionnelle à la quantité de variation entre les groupes. Au sein de l'échantillon, la variance est due au dérangement aléatoire inexpliqué alors qu'un traitement différent peut entraîner une variance entre échantillons.
Avec l’utilisation de cette technique, nous testons une hypothèse nulle (H0) où toutes les moyennes de population sont les mêmes, ou hypothèse alternative (H1) dont au moins une moyenne de population est différente.
Principales différences entre le test T et l’ANOVA
Les différences significatives entre le test T et l'ANOVA sont discutées en détail dans les points suivants:
- Un test d'hypothèse utilisé pour comparer les moyennes de deux populations est appelé test t. Une technique statistique utilisée pour comparer les moyennes de plus de deux populations est appelée analyse de variance ou ANOVA..
- La statistique de test pour le test T est:
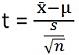 La statistique de test pour ANOVA est:
La statistique de test pour ANOVA est: 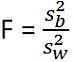
Conclusion
Après avoir examiné les points ci-dessus, on peut dire que le test t est un type particulier d’ANOVA qui peut être utilisé lorsque nous n’avons que deux populations pour comparer leurs moyennes. Bien que les risques d'erreur puissent augmenter si le test t est utilisé lorsqu'il est nécessaire de comparer simultanément plus de deux moyennes des populations, c'est pourquoi l'ANOVA est utilisé.
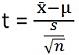 La statistique de test pour ANOVA est:
La statistique de test pour ANOVA est: