Comment trouver les asymptotes d'une hyperbole
 Share
Share
Hyperbole
L'hyperbole est une conique. Le terme hyperbole fait référence aux deux courbes déconnectées montrées dans la figure.
Si les axes principaux coïncident avec les axes cartésiens, l'équation générale de l'hyperbole est de la forme:

Ces hyperboles sont symétriques autour de l’axe des y et sont appelées hyperboles à axe des y. Les hyperboles symétriques autour de l’axe des x (ou hyperbole des abscisses) sont données par l’équation,
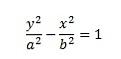 Comment trouver les asymptotes d'une hyperbole
Comment trouver les asymptotes d'une hyperbole
Pour trouver les asymptotes d'une hyperbole, utilisez une simple manipulation de l'équation de la parabole.
je. Apportez d'abord l'équation de la parabole à la forme donnée ci-dessus
Si la parabole est donnée comme mx2+New York2=l, en définissant
une= √ (l/m) et b= √ (-l/n) où l<0
(Cette étape n’est pas nécessaire si l’équation est donnée en standard à partir de.

ii. Ensuite, remplacez le côté droit de l’équation par zéro.

iii. Factoriser l'équation et prendre des solutions

Par conséquent, les solutions sont ,

Les équations des asymptotes sont

Les équations des asymptotes pour l'hyperbole de l'axe des abscisses peuvent également être obtenues par la même procédure.
Trouver les asymptotes d'une hyperbole - Exemple 1
Considérons l'hyperbole donnée par l'équation x2/ 4-y2/ 9 = 1. Trouvez les équations des asymptotes.

Réécrire l'équation et suivre la procédure ci-dessus.
X2/ 4-y2/ 9 = x2/ 22 -y2/ 32 = 1
En remplaçant le côté droit par zéro, l'équation devient x2/ 22 -y2/ 32 = 0.
Factorisation et résolution de l’équation donnent,
(x / 2-y / 3) (x / 2 + y / 3) = 0
Les équations des asymptotes sont,
3x-2y = 0 et 3x + 2y = 0
Trouver les asymptotes d'une hyperbole - Exemple 2
- L'équation d'une parabole est donnée comme -4x² + y² = 4

Cette hyperbole est une hyperbole à axe x.
Réorganiser les termes de l'hyperbole dans la norme de donne
-4x2+ y2= 4 => y2/ 22 -X2/12 = 1
La factorisation de l'équation fournit ce qui suit
(y / 2-x) (y / 2 + x) = 0
Par conséquent, les solutions sont y-2x = 0 et y + 2x = 0.
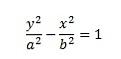 Comment trouver les asymptotes d'une hyperbole
Comment trouver les asymptotes d'une hyperbole 